
Statisticians often make transformations of the data (e.g. The means of the distribution of y at each x value can be connected by a straight line y = mx + c.Īssumptions behind least squares regression analysis The distribution of y given a value of x has equal standard deviation for all x values and is centred about the least squares regression line LSR makes four important assumptions:įor each x i, there are an infinite number of possible values of y, which are Normally distributed It is probably particularly common because the analysis mathematics are simple (because of the Normality assumption), rather than it being a very common rule for the relationship between variables. Simple least squares linear regression is a very standard statistical analysis techniques, particularly when one has little or no idea of the relationship between the x and y variables. Where m is the slope of the line and c is the y-axis intercept and s is the standard deviation of the variation of y about this line. If we assume that the error terms are Normally distributed, the equation reduces to: Simple least squares linear regression assumes that there is only one independent variable x. = the regression slope for the variable x j and the difference between the observed y values and that predicted by the model) = the i th observed value of the dependent variable y = the i th observed value of the independent variable x j
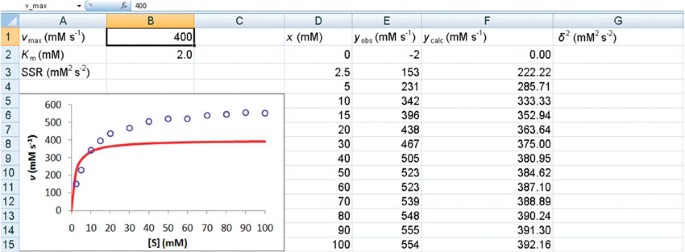
The purpose of least squares linear regression is to represent the relationship between one or more independent variables x 1, x 2, and a variable y that is dependent upon them in the following form: See also: The basics of probability theory introduction, Estimating model parameters from data


 0 kommentar(er)
0 kommentar(er)
